Table of Contents
Introduction to Linked List
A linked list is a fundamental data structure in computer science used for storing and organizing data in a linear sequence. Unlike arrays, linked lists do not require contiguous memory allocation, allowing for dynamic resizing and flexible memory management. In a linked list, elements, known as nodes, are connected through pointers or references, forming a chain-like structure. Each node contains a data element and a reference to the next node in the sequence. This structure allows for efficient insertion and deletion operations at any position in the list. Linked lists come in various types, including singly linked lists, doubly linked lists, and circular linked lists, each with its own characteristics and advantages. Understanding linked lists is essential for mastering data structures and algorithms, as they serve as the foundation for many advanced data structures and algorithms. In this guide, we’ll explore the concepts, operations, and applications of linked lists, providing a comprehensive understanding of this powerful data structure.
Basic Characteristics Linked List
The basic characteristics of a linked list include:
- Dynamic Size: Linked lists can dynamically grow or shrink in size during runtime. Unlike arrays, linked lists do not have a fixed size and can accommodate elements as needed.
- Node Structure: A linked list is composed of nodes, where each node contains a data element and a reference (or pointer) to the next node in the sequence. This structure allows for efficient traversal of the list and facilitates dynamic memory allocation.
- Sequential Access: Linked lists provide sequential access to elements, meaning elements are accessed one after another in a linear order. Traversal of a linked list typically starts from the head (or first) node and progresses through subsequent nodes.
- Dynamic Memory Allocation: Linked lists allocate memory for each node dynamically as elements are added to the list. This dynamic memory allocation allows for efficient use of memory and avoids the need for contiguous memory allocation.
- Insertion and Deletion Flexibility: Linked lists offer efficient insertion and deletion operations at any position within the list. Insertion and deletion operations can be performed in constant time complexity, making linked lists suitable for scenarios requiring frequent modifications.
- No Contiguous Memory Requirement: Unlike arrays, linked lists do not require contiguous memory allocation. Each node in a linked list can be located at any memory address, allowing for flexible memory management.
- Pointer-based Structure: Linked lists are implemented using pointers or references to connect nodes. These pointers establish the relationship between nodes and enable efficient traversal and manipulation of the list.
Understanding these basic characteristics of linked lists is essential for effectively utilizing them in various programming scenarios and data processing tasks.
Comparison of Linked List with Other Data Structures
Here is a comparison of linked lists with other data structures
| Characteristic | Linked List | Array | Stack | Queue | Hash Table |
|---|---|---|---|---|---|
| Memory Allocation | Dynamic, non-contiguous memory allocation | Static, contiguous memory allocation | Static, contiguous memory allocation | Static, contiguous memory allocation | Dynamic, non-contiguous memory allocation |
| Insertion/Deletion | Efficient insertion/deletion at any position | Inefficient insertion/deletion in the middle | Efficient insertion/deletion at one end | Efficient insertion/deletion at both ends | Depends on implementation |
| Access Time | Linear time for traversal and access | Constant time for access | Constant time for access | Constant time for access | Constant time for access |
| Random Access | No, sequential access only | Yes, efficient random access | No | No | No |
| Size Flexibility | Dynamic, size can grow or shrink | Fixed size, cannot dynamically change | Dynamic, size can grow | Dynamic, size can grow | Dynamic, size can grow |
| Implementation | Implemented using pointers or references | Implemented using contiguous memory blocks | Implemented using arrays | Implemented using arrays or linked lists | Implemented using arrays or linked lists |
| Memory Overhead | Additional memory overhead for pointers | Minimal overhead | Minimal overhead | Minimal overhead | Additional memory overhead for pointers |
| Use Cases | Dynamic data storage, frequent insertions | Static data storage, efficient random access | Function call management, expression evaluation | Buffer management, task scheduling | Key-value storage, dictionary operations |
Types of Linked List
There is mainly 4 key types of Linked List
- Singly linked list
- Doubly linked list
- Circular linked list
- Circular doubly linked lists
Singly linked list
A singly linked list is a type of linked list where each node contains a data element and a reference (or pointer) to the next node in the sequence. In a singly linked list, traversal is only possible in one direction, typically from the head (or first) node to the tail (or last) node. Each node in a singly linked list contains two fields a data field to store the element and a next field to store the reference to the next node.

Characteristics of Singly Linked List:
- Node Structure: Each node in a singly linked list contains a data element and a pointer/reference to the next node in the sequence.
- Head Pointer: The singly linked list maintains a reference to the head node, which serves as the starting point for traversal.
- Tail Pointer (Optional): Some implementations of singly linked lists may maintain a reference to the tail node for efficient insertion at the end of the list.
- Traversal: Traversal of a singly linked list is typically performed sequentially from the head node to the tail node.
- Insertion: Singly linked lists support efficient insertion operations, including insertion at the beginning, end, or at any specific position within the list.
- Deletion: Deletion operations in singly linked lists involve removing a node from the list, updating pointers to maintain the integrity of the list structure.
- Dynamic Size: Singly linked lists can dynamically grow or shrink in size during runtime, allowing for flexible memory management.
- Memory Efficiency: Singly linked lists have minimal memory overhead compared to other data structures like arrays, as they only require memory for storing the data and pointers to the next node.
- Space Complexity: Singly linked lists have a space complexity of O(n), where n is the number of elements in the list, as they require memory allocation for each node.
Singly linked lists are commonly used in various applications, including dynamic memory allocation, implementation of stacks, queues, and hash tables, and as the underlying data structure for more complex data structures like graphs and trees. Understanding the characteristics and operations of singly linked lists is essential for mastering data structures and algorithms in computer science.
Doubly linked list
A doubly linked list is a type of linked list in which each node contains two references (pointers) – one to the next node in the sequence and another to the previous node. This structure allows for traversal in both forward and backward directions.
Here’s an overview of doubly linked lists:
Node Structure: Each node in a doubly linked list contains three fields:
- Data: Holds the value or data associated with the node.
- Next Pointer: Points to the next node in the sequence.
- Previous Pointer: Points to the previous node in the sequence.
Advantages:
- Bidirectional Traversal: Allows traversal in both forward and backward directions, enabling efficient operations like reverse traversal and deletion.
- Efficient Insertion and Deletion: Insertion and deletion operations can be more efficient compared to singly linked lists, as they require fewer pointer adjustments.
Operations:
- Insertion:
- Insertion at the beginning: Adjust pointers to include the new node as the first node.
- Insertion at the end: Traverse to the last node and adjust pointers to include the new node.
- Insertion at a specific position: Traverse to the desired position and adjust pointers accordingly.
- Deletion:
- Deletion at the beginning: Update pointers to exclude the first node.
- Deletion at the end: Traverse to the last node and update pointers to exclude it.
- Deletion of a specific node: Adjust pointers of surrounding nodes to bypass the node to be deleted.
- Traversal: Traverse the list in both forward and backward directions by following the next and previous pointers of each node.
Space Complexity: Similar to singly linked lists, the space complexity of a doubly linked list is O(n), where n is the number of nodes in the list. Each node requires memory for storing data and two pointers.
Applications:
- Doubly linked lists are used in scenarios where bidirectional traversal is required, such as in text editors for implementing undo/redo functionality.
- They are also used in data structures like queues and deques (double-ended queues) to support efficient insertion and deletion operations at both ends.
Overall, doubly linked lists offer bidirectional traversal and efficient insertion and deletion operations, making them suitable for various applications where these features are required. However, they have higher memory overhead compared to singly linked lists due to the additional pointers stored in each node.
Circular Linked List
A circular linked list is a variation of a linked list in which the last node points back to the first node, forming a circular structure. This circular connectivity allows for traversal starting from any node and looping back to the beginning.
Here’s an overview of circular linked lists:
Node Structure: Each node in a circular linked list contains two fields:
- Data: Holds the value or data associated with the node.
- Next Pointer: Points to the next node in the sequence.
Advantages:
- Circular Connectivity: Enables traversal starting from any node and looping back to the beginning, offering more flexibility in traversal.
- Implementation Simplicity: Implementation of circular linked lists is often simpler than other types of linked lists as there is no need to maintain a separate reference to the last node.
Operations:
- Insertion:
- Insertion at the beginning: Adjust pointers to include the new node as the first node, updating both the head and tail pointers if needed.
- Insertion at the end: Similar to insertion at the beginning, but also update the tail pointer to maintain circular connectivity.
- Insertion at a specific position: Traverse to the desired position and adjust pointers accordingly.
- Deletion:
- Deletion at the beginning: Update pointers to exclude the first node, updating both the head and tail pointers if needed.
- Deletion at the end: Similar to deletion at the beginning, but also update the tail pointer to maintain circular connectivity.
- Deletion of a specific node: Adjust pointers of surrounding nodes to bypass the node to be deleted.
- Traversal: Traverse the list starting from any node and loop back to the beginning, continuing until all nodes are visited.
Space Complexity: Similar to other types of linked lists, the space complexity of a circular linked list is O(n), where n is the number of nodes in the list. Each node requires memory for storing data and a pointer to the next node.
Applications:
- Circular linked lists are used in scenarios where circular traversal is required, such as in round-robin scheduling algorithms for task distribution.
- They can also be used in applications where elements need to be accessed in a circular manner, such as in the implementation of circular buffers or queues.
Overall, circular linked lists offer circular connectivity and flexible traversal, making them suitable for various applications where these features are required. They are particularly useful in scenarios where elements need to be accessed cyclically or traversed in a circular manner.
Circular Doubly Linked Lists
A circular doubly linked list is a type of linked list where each node has two pointers: one pointing to the next node and another pointing to the previous node. Additionally, the last node’s “next” pointer points to the first node, and the first node’s “previous” pointer points to the last node, forming a circular structure.
Here’s an overview of circular doubly linked lists:
Node Structure: Each node in a circular doubly linked list contains three fields:
- Data: Holds the value or data associated with the node.
- Next Pointer: Points to the next node in the sequence.
- Previous Pointer: Points to the previous node in the sequence.
Advantages:
- Bidirectional Traversal: Allows traversal in both forward and backward directions, enabling efficient operations like reverse traversal and deletion.
- Circular Connectivity: Enables traversal starting from any node and looping back to the beginning or end of the list.
Operations:
- Insertion:
- Insertion at the beginning: Adjust pointers to include the new node as the first node, updating both the head and tail pointers if needed.
- Insertion at the end: Similar to insertion at the beginning, but also update the tail pointer to maintain circular connectivity.
- Insertion at a specific position: Traverse to the desired position and adjust pointers accordingly.
- Deletion:
- Deletion at the beginning: Update pointers to exclude the first node, updating both the head and tail pointers if needed.
- Deletion at the end: Similar to deletion at the beginning, but also update the tail pointer to maintain circular connectivity.
- Deletion of a specific node: Adjust pointers of surrounding nodes to bypass the node to be deleted.
- Traversal: Traverse the list in both forward and backward directions by following the next and previous pointers of each node.
Space Complexity: The space complexity of a circular doubly linked list is O(n), where n is the number of nodes in the list. Each node requires memory for storing data and two pointers.
Applications:
- Circular doubly linked lists are used in scenarios where bidirectional traversal and circular connectivity are required, such as in the implementation of circular buffers, queues, and navigational structures.
- They are also useful in applications where elements need to be accessed cyclically or traversed in both forward and backward directions.
Overall, circular doubly linked lists offer bidirectional traversal, circular connectivity, and efficient insertion and deletion operations, making them suitable for various applications where these features are required. They are particularly useful in scenarios where elements need to be accessed cyclically or traversed in both forward and backward directions.
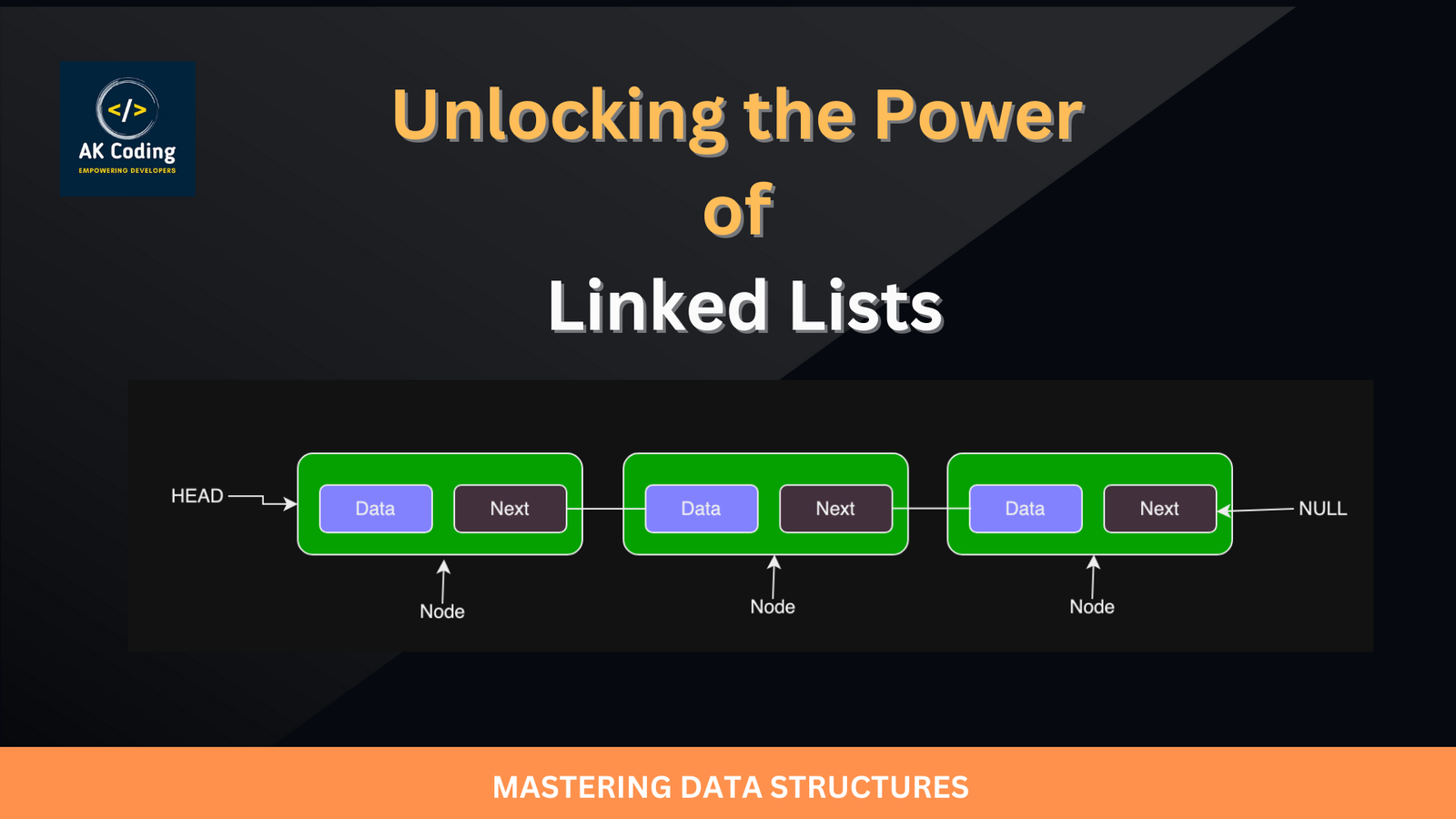
Anatomy of a Linked List
The anatomy of a linked list refers to its fundamental components and structure. At its core, a linked list comprises nodes, each containing data and a reference to the next node. This arrangement forms a linear sequence where nodes are connected via pointers, facilitating efficient traversal and manipulation. Understanding the anatomy of a linked list involves recognizing its node-based architecture, pointer-based connections, and the role of special nodes like the head and tail. By grasping these key elements, developers can effectively harness the versatility and power of linked lists in various programming scenarios.
Linked List Node Structure and Pointers (Next and Previous)
The node structure of a linked list defines the blueprint for each element (or node) in the linked list. Each node contains two fields: a data field to store the actual data and a pointer/reference field to store the reference to the next node in the sequence. Here’s how the node structure is typically defined:
Node Structure:
----------------
| Data | Next Pointer |
----------------- Data Field: This field stores the actual data or payload associated with the node. It can hold any type of data, such as integers, characters, strings, or custom objects, depending on the requirements of the linked list.
- Next Pointer/Reference: This field is a pointer or reference that points to the next node in the sequence. It establishes the link between nodes and allows for traversal of the linked list. In a singly linked list, each node contains a single next pointer that points to the next node in the sequence. In a doubly linked list, each node contains two pointers: one to the next node and one to the previous node.
The node structure defines the fundamental building block of the linked list data structure. It encapsulates both the data element and the link to the next node, allowing for efficient traversal and manipulation of the list. By defining a consistent node structure, linked lists can accommodate elements of varying data types and sizes, making them versatile and flexible data structures for various programming tasks.
Linked List Head and Tail Pointers
In a linked list, the head and tail pointers are references to the first and last nodes of the list, respectively. These pointers are crucial for maintaining the structure of the linked list and enabling efficient traversal and manipulation operations.
Linked List Head Pointer
- The head pointer points to the first node in the linked list.
- It serves as the starting point for traversal and manipulation operations on the list.
- The head pointer is used to access the first element of the list and facilitates operations such as insertion, deletion, and traversal.
Linked List Tail Pointer
- The tail pointer points to the last node in the linked list.
- It allows for efficient insertion operations at the end of the list.
- In some implementations of linked lists, the tail pointer may be optional, especially in singly linked lists where maintaining a reference to the tail node may not be necessary for all operations.
- The tail pointer is particularly useful for operations that involve appending elements to the end of the list or performing operations on the last element.
Having both head and tail pointers provides flexibility and efficiency in performing various operations on the linked list. While the head pointer is essential for accessing the beginning of the list and performing operations at the front, the tail pointer facilitates efficient operations at the end of the list. Together, these pointers enable efficient traversal, insertion, deletion, and manipulation of the linked list, making them essential components of the data structure.
Linked List Operations
Linked lists support various operations for managing and manipulating the elements in the list. Here are some common operations performed on linked lists:
Insertion
- Insertion at the Beginning: Add a new node at the beginning of the list, updating the head pointer.
- Insertion at the End: Append a new node at the end of the list, updating the tail pointer if present.
- Insertion at a Specific Position: Insert a new node at a specific position in the list, adjusting pointers to maintain connectivity.
Deletion
- Deletion at the Beginning: Remove the first node from the list, updating the head pointer.
- Deletion at the End: Remove the last node from the list, updating the tail pointer if present.
- Deletion of a Specific Node: Remove a node at a specific position in the list, adjusting pointers to maintain connectivity.
Traversal
- Forward Traversal: Visit each node in the list sequentially from the head to the tail, performing operations as needed.
- Backward Traversal (for Doubly Linked Lists): Traverse the list in reverse order, starting from the tail and moving towards the head.
Searching
- Linear Search: Search for a specific value or element in the list by traversing the nodes sequentially until a match is found.
- Binary Search (for Sorted Linked Lists): If the linked list is sorted, perform a binary search to find the target element efficiently.
Updating/Modifying Nodes
- Update the value of a node at a specific position in the list.
- Modify the data or attributes of a node without changing its position in the list.
Reversing the Linked List
- Reverse the order of nodes in the list, updating pointers to maintain connectivity.
Finding the Middle Node
- Find the middle node of the list, which can be useful for various algorithms and operations.
Concatenation
- Combine two linked lists into a single linked list, connecting the end of the first list to the beginning of the second list.
These operations are fundamental for managing linked lists and are used extensively in various applications and algorithms. The choice of operation depends on the specific requirements and objectives of the program or algorithm being implemented.
Advantages and Disadvantages of Linked Lists
Linked lists offer several advantages and disadvantages compared to other data structures like arrays. Here’s a summary of the key advantages and disadvantages of linked lists:
Advantages:
- Dynamic Size: Linked lists can dynamically grow or shrink in size during runtime, allowing for efficient memory utilization and flexible data storage.
- Dynamic Memory Allocation: Nodes in a linked list are allocated memory dynamically, enabling efficient memory management and eliminating the need for contiguous memory allocation.
- Insertion and Deletion: Linked lists support efficient insertion and deletion operations at any position in the list, without requiring elements to be shifted.
- Memory Efficiency: Linked lists have minimal memory overhead compared to arrays, as they only require memory for storing data and pointers to the next node.
- Flexibility: Linked lists can accommodate elements of varying data types and sizes, making them versatile and flexible for various programming tasks.
- Efficient Operations: Certain operations, such as insertion and deletion, can be performed in constant time complexity, making linked lists suitable for scenarios requiring frequent modifications.
Disadvantages:
- Sequential Access: Linked lists provide sequential access to elements, meaning traversal must be performed sequentially from the beginning of the list to access specific elements. This can result in slower access times compared to arrays, which offer direct random access to elements.
- Memory Overhead: Linked lists require additional memory overhead for storing pointers/references to the next node, which can increase memory consumption, especially for large lists with many nodes.
- No Random Access: Unlike arrays, linked lists do not support efficient random access to elements. Accessing elements at arbitrary positions in the list requires traversal from the beginning, resulting in slower access times for large lists.
- Traversal Overhead: Traversing a linked list involves following pointers from one node to the next, which can introduce overhead, especially for large lists with many nodes.
- Memory Fragmentation: Dynamic memory allocation and deallocation in linked lists can lead to memory fragmentation over time, which may impact overall system performance and memory usage.
- Lack of Cache Locality: Linked lists do not exhibit good cache locality, as nodes may be scattered in memory, leading to cache misses and slower performance in some scenarios.
Overall, linked lists are valuable data structures that offer advantages in terms of flexibility, dynamic memory management, and efficient insertion/deletion operations. However, they also have limitations in terms of access times, memory overhead, and traversal efficiency, which should be considered when choosing the appropriate data structure for a given application or problem.
Applications of Linked Lists
Linked lists find applications in various domains due to their flexibility and dynamic memory allocation. Some common applications of linked lists include:
- Dynamic Memory Allocation: Linked lists are used in dynamic memory allocation scenarios, such as implementing memory pools, dynamic memory management, and garbage collection algorithms.
- Data Structures: Linked lists serve as the foundation for implementing other complex data structures such as stacks, queues, graphs, and hash tables.
- File Systems: Linked lists are employed in file systems to maintain directory structures and manage file blocks efficiently. Each directory entry or file block can be represented as a node in a linked list.
- Undo Functionality: Linked lists are used to implement undo functionality in text editors and graphics software. Each action performed by the user can be stored as a node in a linked list, allowing for easy reversal of actions.
- Polynomial Manipulation: Linked lists are used to represent polynomials in mathematics and computer science. Each term in a polynomial can be represented as a node in a linked list, allowing for easy addition, subtraction, multiplication, and evaluation of polynomials.
- Task Scheduling: Linked lists are utilized in task scheduling algorithms to manage job queues and prioritize tasks based on their deadlines, priorities, or other criteria.
- Sparse Matrices: Linked lists are employed to represent sparse matrices, where most of the elements are zero. Each non-zero element is stored as a node in a linked list, allowing for efficient storage and manipulation of sparse matrices.
- Symbol Tables: Linked lists are used in symbol tables and associative arrays to store key-value pairs. Each key-value pair can be stored as a node in a linked list, allowing for efficient lookup, insertion, and deletion operations.
- Music and Playlist Management: Linked lists are utilized in music and playlist management applications to organize and manage playlists. Each song or track can be represented as a node in a linked list, allowing for easy addition, removal, and rearrangement of songs.
- Network Routing: Linked lists are used in network routing algorithms to maintain routing tables and manage routing paths efficiently.
These are just a few examples of the diverse applications of linked lists in various fields. Their flexibility, dynamic memory allocation, and efficient insertion/deletion operations make them suitable for a wide range of scenarios where dynamic data storage and manipulation are required.
Implementation of Linked List in Java
Here’s a basic implementation of a singly linked list in Java:
// Node class to represent individual nodes in the linked list
class Node {
int data; // Data stored in the node
Node next; // Reference to the next node
// Constructor to initialize a new node
public Node(int data) {
this.data = data;
this.next = null;
}
}
// Linked list class to define operations on the linked list
public class LinkedList {
private Node head; // Reference to the head (first node) of the linked list
// Constructor to initialize an empty linked list
public LinkedList() {
this.head = null;
}
// Method to insert a new node at the beginning of the linked list
public void insertAtBeginning(int data) {
Node newNode = new Node(data); // Create a new node with the given data
newNode.next = head; // Set the next pointer of the new node to the current head
head = newNode; // Update the head to point to the new node
}
// Method to insert a new node at the end of the linked list
public void insertAtEnd(int data) {
Node newNode = new Node(data); // Create a new node with the given data
if (head == null) { // If the list is empty, set the new node as the head
head = newNode;
return;
}
Node current = head;
while (current.next != null) { // Traverse to the end of the list
current = current.next;
}
current.next = newNode; // Set the next pointer of the last node to the new node
}
// Method to display the elements of the linked list
public void display() {
Node current = head; // Start traversal from the head
while (current != null) { // Traverse until the end of the list
System.out.print(current.data + " "); // Print the data of the current node
current = current.next; // Move to the next node
}
System.out.println();
}
// Main method to test the implementation
public static void main(String[] args) {
LinkedList list = new LinkedList(); // Create a new linked list
list.insertAtEnd(10); // Insert elements into the list
list.insertAtEnd(20);
list.insertAtEnd(30);
list.insertAtBeginning(5);
list.display(); // Display the elements of the list
}
}This implementation provides basic functionalities such as insertion at the beginning and end of the list, as well as displaying the elements of the list. You can further extend this implementation to include additional operations such as deletion, searching, and more.
Linked List Performance Analysis and Time Complexity
Performance analysis of a linked list involves evaluating the time complexity of various operations performed on the linked list. Here’s a summary of the time and space complexity of common operations in a singly linked list:
Linked List Time Complexity
Insertion at the Beginning (prepend):
- Time Complexity: O(1)
- Inserting a new node at the beginning of the linked list involves updating the head pointer to point to the new node. This operation can be performed in constant time, regardless of the size of the list.
Insertion at the End (append):
- Time Complexity: O(n)
- Inserting a new node at the end of the linked list requires traversing the entire list to find the last node. Therefore, the time complexity is linear in the size of the list.
Insertion at a Specific Position:
- Complexity: O(n)
- Explanation: Inserting a new node at a specific position in the linked list requires traversing the list to find the node at the specified position. Therefore, the time complexity is linear in the size of the list.
Deletion at the Beginning:
- Time Complexity: O(1)
- Deleting the first node in the linked list involves updating the head pointer to point to the next node. This operation can be performed in constant time, regardless of the size of the list.
Deletion at the End:
- Time Complexity: O(n)
- Deleting the last node in the linked list requires traversing the entire list to find the second-to-last node. Therefore, the time complexity is linear in the size of the list.
Deletion of a Specific Node:
- Time Complexity: O(n)
- Deleting a specific node in the linked list requires traversing the list to find the node to be deleted. Therefore, the time complexity is linear in the size of the list.
Traversal:
- Time Complexity: O(n)
- Traversing the entire linked list to access each node’s data involves visiting each node once. Therefore, the time complexity is linear in the size of the list.
Searching:
- Time Complexity: O(n)
- Searching for a specific element in the linked list requires traversing the list to find the desired node. Therefore, the time complexity is linear in the size of the list.
Overall, linked lists offer efficient insertion and deletion operations at the beginning of the list but may have less efficient performance for operations such as insertion at the end, deletion at the end, and searching, which require traversing the entire list. The choice of data structure should consider the specific requirements and performance characteristics of the application or algorithm being implemented.
Linked List Space Complexity
The space complexity of a linked list depends on several factors, including the number of nodes in the list and the implementation details of the linked list. Here’s a summary of the space complexity of a singly linked list:
Node Overhead:
- Each node in the linked list requires space to store its data and a reference/pointer to the next node.
- In Java, for example, each object has an overhead for storing its fields, header information, and alignment padding.
- Therefore, the space required for each node is proportional to the size of the data stored in the node and the size of the reference/pointer.
- The space complexity of a single node is typically O(1), as it does not depend on the size of the list.
Total Space:
- The total space required for the linked list is the sum of the space required for each node.
- If the linked list contains n nodes, the total space complexity is proportional to the number of nodes in the list.
- Therefore, the space complexity of the entire linked list is O(n), where n is the number of nodes in the list.
Additional Overhead:
- In addition to the space required for storing node data and references, there may be additional overhead associated with managing the linked list, such as maintaining pointers to the head and tail nodes.
- The space required for this additional overhead is typically constant and does not depend on the size of the list.
- Therefore, it does not significantly impact the overall space complexity of the linked list.
Overall, the space complexity of a singly linked list is O(n), where n is the number of nodes in the list. Linked lists offer dynamic memory allocation, allowing for efficient memory utilization, especially in scenarios where the size of the list may change dynamically during runtime. However, they may have higher memory overhead compared to arrays due to the need for storing pointers/references to connect nodes.
Linked List Best Practices and Tips
Here are some best practices and tips for working with linked lists effectively:
- Choose the Right Type of Linked List: Depending on your requirements, choose between singly linked lists, doubly linked lists, or circular linked lists. Each type has its own advantages and trade-offs.
- Use Dummy Nodes: In some scenarios, using dummy nodes (sentinels) at the beginning or end of the list can simplify insertion and deletion operations, especially at the edge cases.
- Be Mindful of Edge Cases: Always handle edge cases such as an empty list, a list with only one node, or operations at the beginning or end of the list gracefully to avoid errors.
- Avoid Memory Leaks: Ensure that you deallocate memory properly when nodes are removed from the list to avoid memory leaks. Failure to do so can lead to inefficient memory usage and degradation of performance.
- Use Iterators or Cursors: When traversing a linked list, consider using iterators or cursors instead of directly manipulating node references. This can make your code cleaner and more readable.
- Avoid Excessive Traversal: Minimize the number of traversals through the list whenever possible, as excessive traversal can lead to performance degradation, especially for large lists.
- Consider Space and Time Complexity: Understand the space and time complexity of different operations on linked lists and choose the appropriate data structure based on your requirements and performance considerations.
- Test Thoroughly: Test your linked list implementation rigorously with various input sizes and scenarios to ensure correctness and performance.
- Implement Reusable Functions: Implement reusable functions for common operations such as insertion, deletion, and traversal to avoid code duplication and improve maintainability.
- Document and Comment: Document your code effectively, including the purpose of each function, the complexity of operations, and any assumptions made. This makes your code more understandable for yourself and other developers.
- Consider Alternatives: Depending on your specific requirements, consider alternative data structures such as arrays or hash tables, which may offer better performance or memory usage in certain scenarios.
By following these best practices and tips, you can effectively work with linked lists and ensure that your code is efficient, reliable, and maintainable.
Conclusion
In conclusion, linked lists are fundamental data structures that offer dynamic memory allocation, efficient insertion and deletion operations, and flexibility in data storage. Whether implementing singly linked lists, doubly linked lists, or circular linked lists, understanding their characteristics, operations, and best practices is crucial for effective use in various programming scenarios.
Linked lists excel in scenarios where dynamic resizing, frequent insertions and deletions, and flexible memory management are required. They serve as the building blocks for implementing more complex data structures such as stacks, queues, graphs, and hash tables.
However, linked lists also have limitations, including sequential access, higher memory overhead compared to arrays, and less efficient random access. It’s essential to consider the specific requirements and performance characteristics of the application or algorithm being implemented when choosing the appropriate data structure.
By following best practices such as handling edge cases, avoiding memory leaks, and optimizing operations, developers can leverage the power of linked lists effectively while ensuring correctness, performance, and maintainability in their codebases. Overall, linked lists remain a valuable tool in the toolkit of any programmer, offering a versatile and efficient solution for dynamic data storage and manipulation.
FAQs
What is a linked list?
A linked list is a linear data structure consisting of a sequence of elements called nodes, where each node contains a data field and a reference (pointer) to the next node in the sequence.
What are the advantages of using linked lists?
Linked lists offer dynamic memory allocation, efficient insertion and deletion operations, and flexibility in data storage. They are particularly useful when the size of the list is not fixed and needs to be adjusted dynamically.
What are the types of linked lists?
There are several types of linked lists, including singly linked lists (each node points to the next node), doubly linked lists (each node points to both the next and previous nodes), and circular linked lists (the last node points back to the first node).
What is the time complexity of operations in a linked list?
The time complexity of operations in a linked list varies depending on the operation and the type of linked list. Generally, insertion and deletion operations at the beginning of a singly linked list have a time complexity of O(1), while insertion and deletion operations at the end have a time complexity of O(n).
What are the drawbacks of linked lists compared to arrays?
Linked lists have some drawbacks compared to arrays, including less efficient random access, higher memory overhead due to the need for storing pointers, and slower traversal times for large lists.
How do you traverse a linked list?
Traversing a linked list involves starting from the head (or first node) of the list and moving to the next node in the sequence until the end of the list is reached. This process is typically done iteratively using a loop.
How do you insert and delete nodes in a linked list?
To insert a node in a linked list, you adjust the pointers of the surrounding nodes to include the new node. To delete a node, you adjust the pointers of the surrounding nodes to bypass the node to be deleted and deallocate its memory.
When should I use a linked list instead of an array?
Linked lists are preferable over arrays when dynamic memory allocation, efficient insertion and deletion operations, or flexibility in data storage are required. They are particularly useful in scenarios where the size of the data structure is not fixed or needs to be adjusted frequently.
Read other awesome articles in Medium.com or in akcoding’s posts.
OR
Join us on YouTube Channel
OR Scan the QR Code to Directly open the Channel 👉

