Table of Contents
Introduction
Queue in Data Structure is a linear data structure that follows the First-In-First-Out (FIFO) principle, where the first element added to the queue is the first one to be removed. It operates with two main operations: enqueue, which adds an element to the end of the queue, and dequeue, which removes an element from the front of the queue. Additionally, queues typically support other operations such as peek (viewing the element at the front without removing it), checking if the queue is empty, and determining its size. Queues find applications in various fields such as computer science, operating system scheduling, network data packet routing, and simulations of real-world scenarios involving waiting lines.
Purpose and Usage in Computer Science
The purpose and usage of queue in computer science are multifaceted and vital across various domains. Here’s a breakdown:
- Data Processing Pipelines: Queues are often employed in data processing pipelines where tasks or data packets need to be processed sequentially. Each stage of the pipeline can be represented by a queue, ensuring orderly and efficient processing of tasks.
- Job Scheduling and Management: Operating systems utilize queues extensively for job scheduling and management. Various scheduling algorithms such as First-Come-First-Served (FCFS), Shortest Job Next (SJN), and Round Robin rely on queues to manage the execution order of processes.
- Breadth-First Search (BFS) in Graphs: Queues play a crucial role in BFS, an algorithm for traversing or searching tree or graph data structures. BFS explores all the neighbor nodes at the present depth prior to moving on to nodes at the next depth level. A queue is used to maintain the nodes to be visited in the order they were discovered.
- Buffering and Data Storage: Queues are fundamental in buffering and managing data flow between different components of a system. For instance, in networking, queues are used for storing data packets temporarily until they can be processed or transmitted further.
- Event Handling and Synchronization: Queues are employed in event-driven programming paradigms for managing event queues. Events are added to the queue as they occur and are processed in the order they were received. This ensures proper synchronization and handling of events in systems like graphical user interfaces (GUIs) and servers.
- Resource Sharing and Synchronization: Queues are utilized for resource sharing and synchronization in concurrent programming. Threads or processes communicate and synchronize their activities through shared queues, ensuring orderly access to shared resources and preventing race conditions.
- Transaction Processing: Queues are used in transaction processing systems to manage requests or transactions waiting to be processed. This ensures fairness and consistency in processing transactions, especially in scenarios with high concurrency and varying processing times.
- Message Queues in Distributed Systems: In distributed systems, message queues facilitate communication and coordination between different components or nodes. They enable asynchronous messaging and decouple producers from consumers, improving system scalability, fault tolerance, and reliability.
In essence, Queue in Data Structure serve as essential tools in computer science for managing data, tasks, events, and resources in an orderly and efficient manner, contributing significantly to the design and optimization of various algorithms and systems.
Importance of Queue in Various Applications
The importance of Queue in Data Structure in various applications stems from their ability to manage and process data or tasks in a structured and efficient manner. Here are some key areas where queues play a crucial role:
- Operating Systems: Queues are fundamental components of operating systems, used for process scheduling, managing I/O requests, handling interrupts, and implementing various synchronization mechanisms. They ensure fair and efficient resource allocation and utilization, contributing to system stability and performance.
- Networking: Queues are indispensable in networking protocols and devices for managing data packet transmission and routing. They are used in routers, switches, and network buffers to store and forward data packets, preventing congestion and ensuring smooth data flow across networks.
- Databases: Queues are employed in database systems for managing transaction processing, query execution, and resource allocation. They help regulate the flow of requests and ensure that transactions are processed in an orderly and consistent manner, maintaining database integrity and reliability.
- Web Servers: Queues are used in web servers to manage incoming requests from clients, such as HTTP requests for web pages or API calls. They help handle concurrent connections efficiently, prevent overloading of server resources, and ensure responsive and scalable web services.
- Parallel and Distributed Computing: Queues play a critical role in parallel and distributed computing environments for task scheduling, load balancing, and inter-process communication. They enable efficient utilization of computing resources, coordination of distributed tasks, and seamless integration of parallel processing algorithms.
- Real-time Systems: Queues are essential in real-time systems for managing time-critical tasks and events. They help prioritize and schedule tasks based on their deadlines, ensuring timely processing and response to external stimuli in applications such as embedded systems, robotics, and control systems.
- Simulation and Modeling: Queues are widely used in simulation and modeling applications to represent waiting lines, service processes, and event sequences. They facilitate the modeling of complex systems with dynamic behavior, enabling the analysis and optimization of performance, resource utilization, and system behavior.
- Financial Systems: Queues are utilized in financial systems for managing transaction queues, order processing, and message queuing in trading platforms, banking systems, and stock exchanges. They help ensure orderly execution of financial transactions, minimize latency, and maintain system integrity and compliance.
In summary, Queue in Data Structure are versatile that find application across a wide range of domains, providing essential functionality for managing data, tasks, and resources in various computational and real-world scenarios. Their importance lies in their ability to improve system efficiency, scalability, responsiveness, and reliability, contributing to the smooth operation of diverse applications and systems.
Basic Concepts of a Queue in Data Structure
FIFO Principle
The FIFO (First-In-First-Out) principle is a fundamental characteristic of queues. It dictates that the first element added to the queue will be the first one to be removed. In other words, the order of insertion is preserved, and elements are processed in the order in which they arrive.
Here’s how the FIFO principle works in a queue:
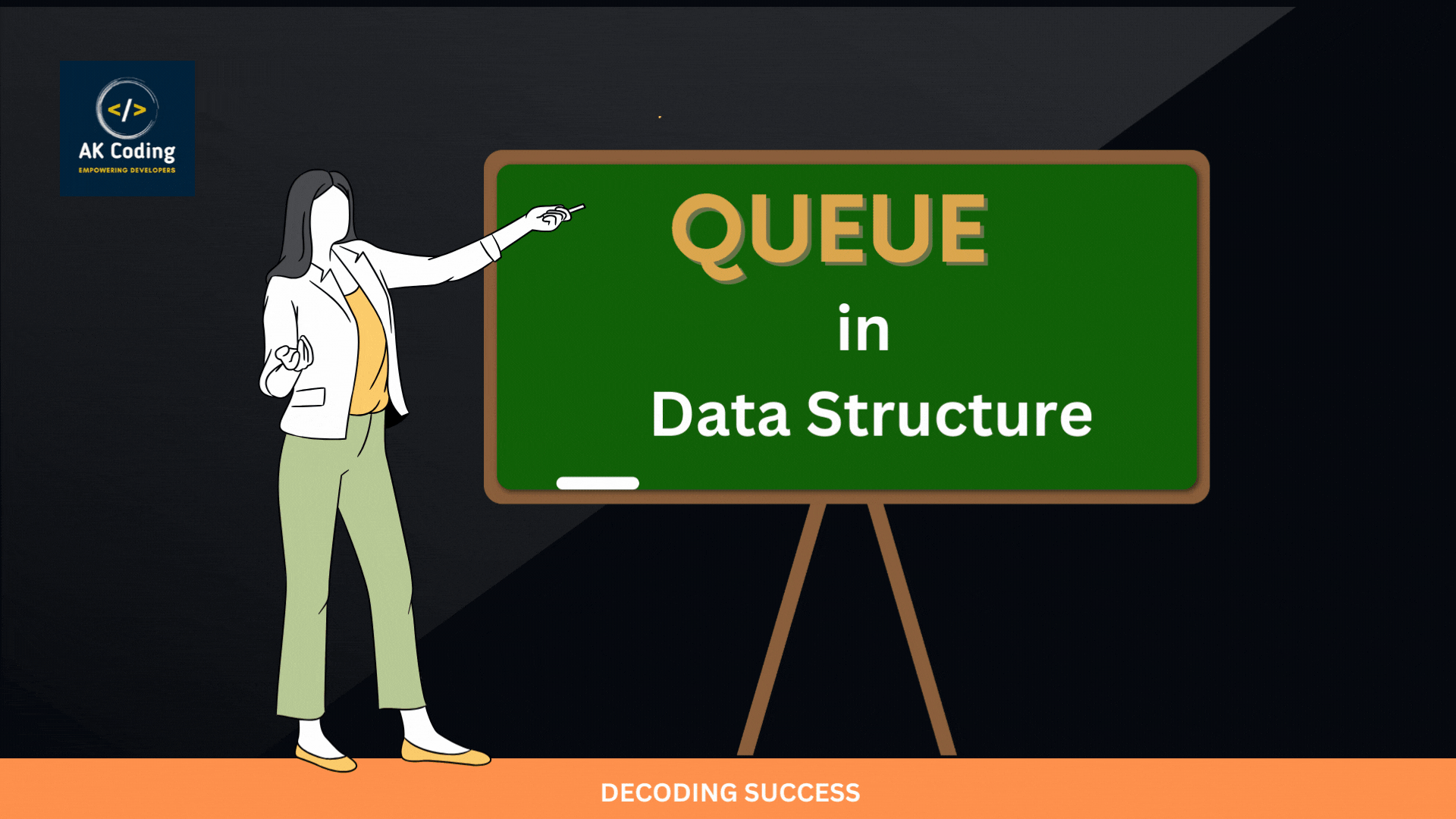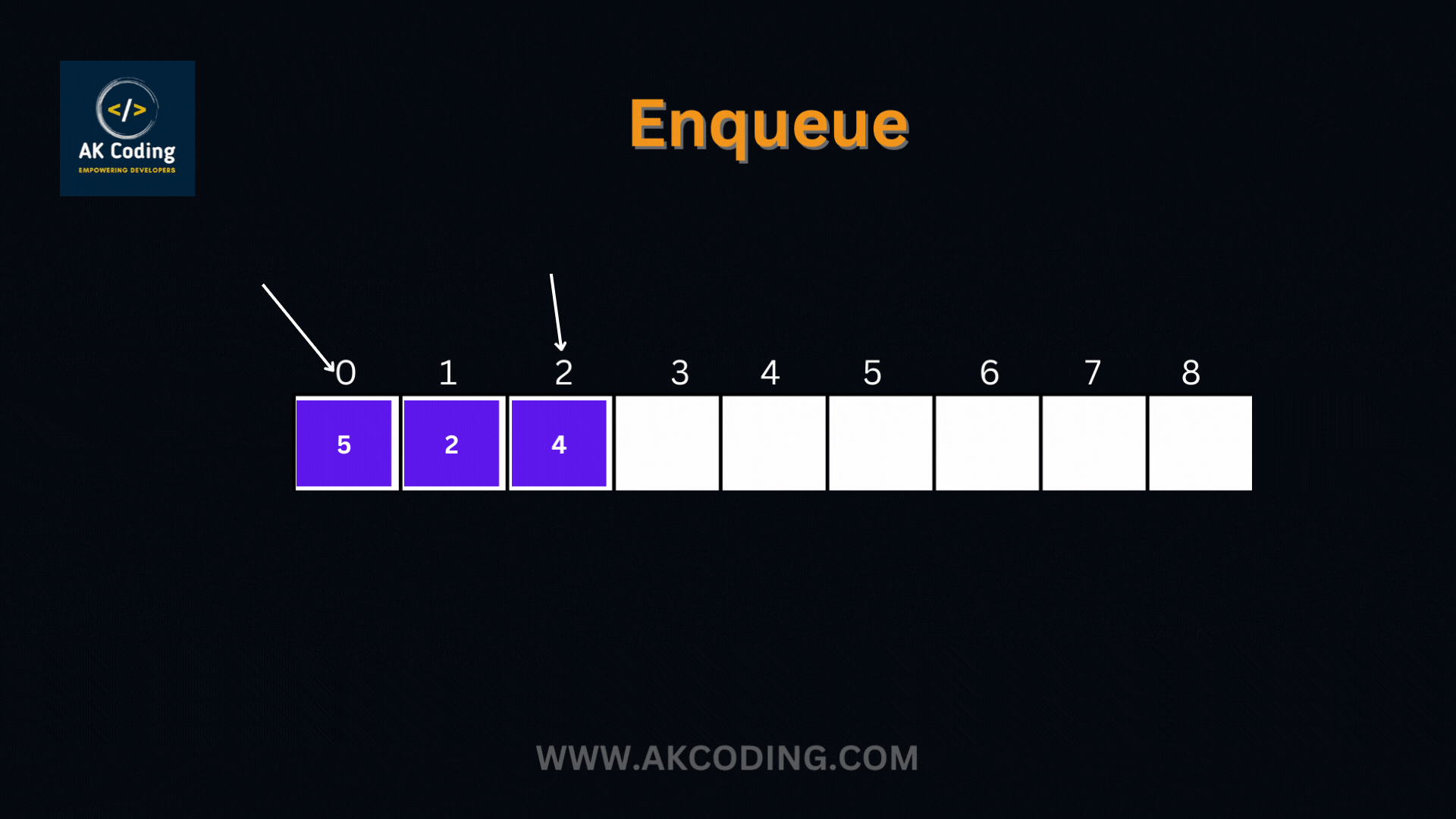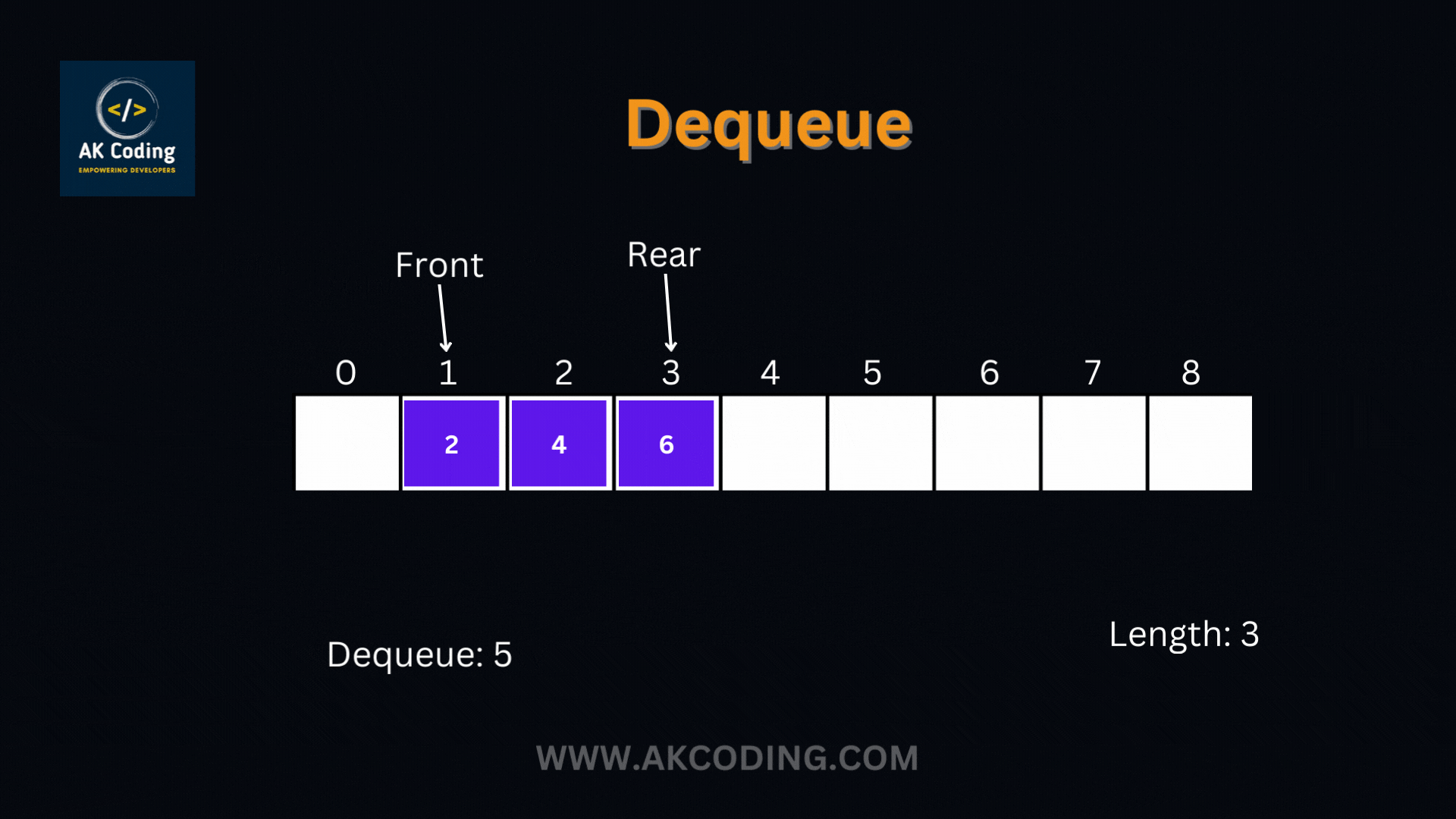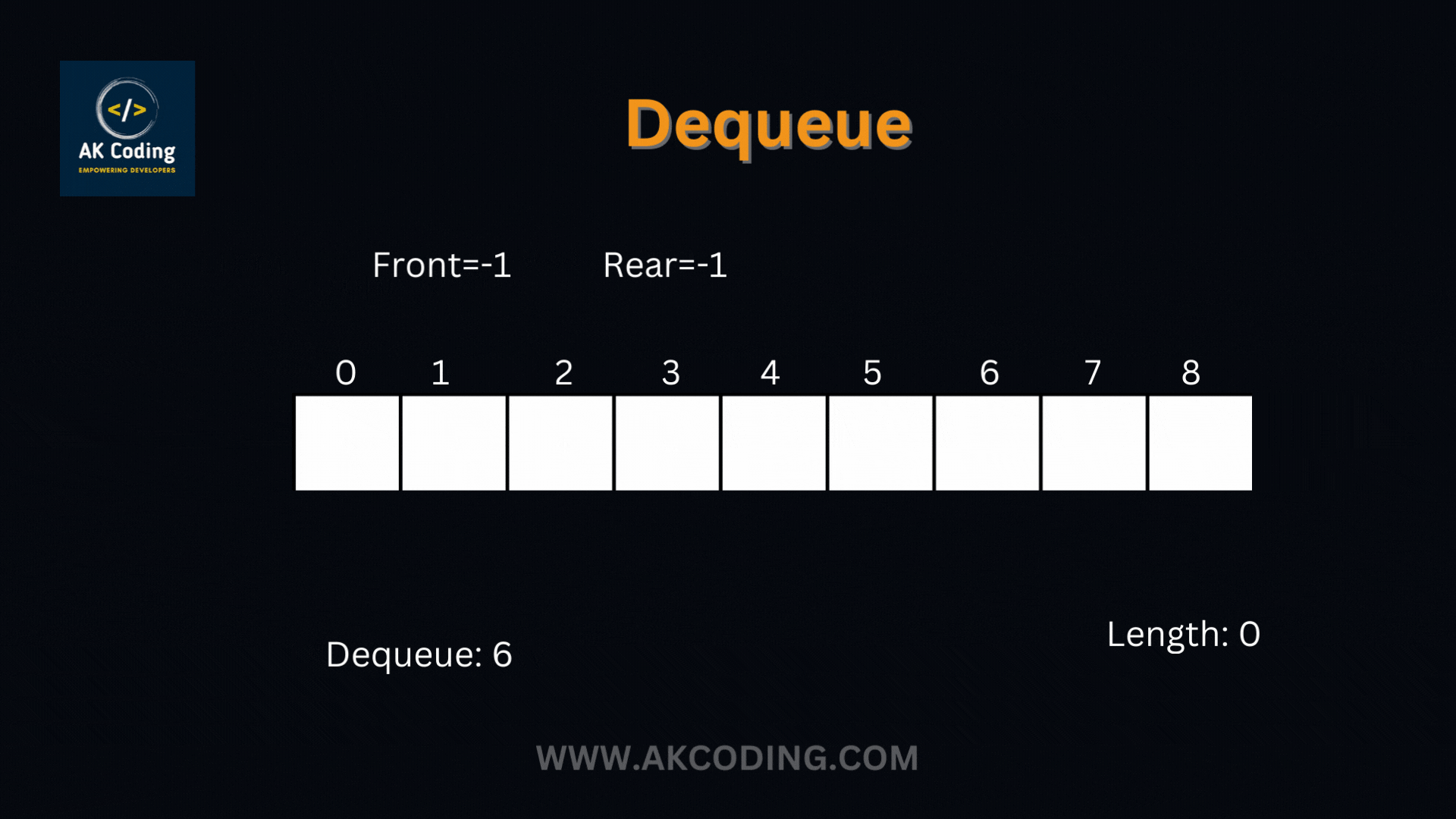
- Enqueue Operation: When an element is added to the queue (via the enqueue operation), it is placed at the rear or end of the queue. If the queue is initially empty, the newly added element becomes the only element in the queue.
- Dequeue Operation: When an element is removed from the queue (via the dequeue operation), the element at the front or head of the queue is removed. This ensures that the oldest element in the queue, i.e., the one that has been waiting the longest, is processed first.
- Order Preservation: The FIFO principle ensures that the order of insertion is maintained throughout the lifetime of the queue. New elements are added at one end of the queue, and existing elements are removed from the other end, preserving the original sequence.
- Usage in Queuing Systems: FIFO is commonly used in queuing systems across various applications, such as operating system scheduling, network packet routing, job processing, and event handling. It ensures fairness and transparency in the processing order, as tasks or data packets are processed in the order they were received.
- Example: Consider a queue representing a line of people waiting to purchase tickets at a movie theater. The first person to arrive (join the queue) will be the first one to purchase a ticket (leave the queue). Subsequent people join the line behind the others, and they are served in the order they arrived, adhering to the FIFO principle.
Overall, the FIFO principle is a fundamental concept in queue in data structure, ensuring that elements are processed in a fair and orderly manner based on their arrival order, which is essential for various applications requiring sequential processing and ordered execution.
Operations Supported by a Queue
Queue in data structure support several fundamental operations for managing and manipulating the data they contain. These operations allow for the insertion, removal, and examination of elements within the queue. The key operations supported by a queue typically include:
- Enqueue (Addition):
- Description: Adds an element to the rear or end of the queue.
- Implementation: The new element is appended to the end of the queue.
- Time Complexity: O(1) – Constant time complexity, assuming no resizing of underlying data structures.
- Dequeue (Removal):
- Description: Removes and returns the element at the front or head of the queue.
- Implementation: The element at the front of the queue is removed and returned.
- Time Complexity: O(1) – Constant time complexity, assuming no resizing of underlying data structures.
- Peek (Examination):
- Description: Retrieves the element at the front or head of the queue without removing it.
- Implementation: Returns the element at the front of the queue without modifying the queue.
- Time Complexity: O(1) – Constant time complexity, as it involves accessing a single element.
- isEmpty (Check if Empty):
- Description: Checks if the queue is empty or contains no elements.
- Implementation: Returns true if the queue is empty; otherwise, returns false.
- Time Complexity: O(1) – Constant time complexity, as it only involves checking the size of the queue.
- Size (Get Size):
- Description: Returns the number of elements currently present in the queue.
- Implementation: Returns the count of elements stored in the queue.
- Time Complexity: O(1) – Constant time complexity, as it only involves retrieving the size metadata.
These operations form the basic interface for interacting with a queue in data structure, allowing for the insertion, removal, and examination of elements while maintaining the FIFO (First-In-First-Out) order. Additionally, various advanced operations and functionalities can be built upon these fundamental operations to extend the capabilities of queues to suit specific application requirements.
Implementation of Queue in Data Structure
A. Array-based Implementation
Overview:
An array-based queue utilizes an array to store elements in a sequential manner. Elements are inserted at the rear end of the array and removed from the front end, adhering to the FIFO principle. The array needs to be dynamically resized when it reaches its capacity to accommodate additional elements.
Operations and Their Time Complexities:
- Enqueue (Addition):
- Description: Adds an element to the rear end of the queue.
- Implementation: Append the new element to the end of the array.
- Time Complexity: O(1) average case, O(n) worst case (when resizing is required).
- Dequeue (Removal):
- Description: Removes and returns the element at the front of the queue.
- Implementation: Remove the element at the front of the array and shift remaining elements.
- Time Complexity: O(n) – Linear time complexity due to shifting elements.
- Peek (Examination):
- Description: Retrieves the element at the front of the queue without removing it.
- Implementation: Access the first element of the array.
- Time Complexity: O(1) – Constant time complexity.
- isEmpty (Check if Empty):
- Description: Checks if the queue is empty.
- Implementation: Check if the array is empty.
- Time Complexity: O(1) – Constant time complexity.
- Size (Get Size):
- Description: Returns the number of elements in the queue.
- Implementation: Return the size of the array.
- Time Complexity: O(1) – Constant time complexity.
Pros:
- Simple Implementation: Array-based queues are relatively easy to implement.
- Random Access: Allows for direct access to elements by index.
- Efficient for Static Size: If the size of the queue is fixed and known in advance, array-based implementation can be efficient.
Cons:
- Dynamic Resizing: Resizing the array when it reaches capacity can be costly, especially for large queues.
- Memory Overhead: May lead to wasted memory if the initial array size is not chosen appropriately.
- Inefficient Dequeue: Removing elements from the front of the array requires shifting remaining elements, leading to linear time complexity.
Simple implementation of an array-based queue in Java:
public class ArrayQueue {
private int[] array;
private int front; // Index of the front element
private int rear; // Index of the rear element
private int size; // Current size of the queue
private int capacity; // Maximum capacity of the queue
// Constructor to initialize the queue with a given capacity
public ArrayQueue(int capacity) {
this.capacity = capacity;
array = new int[capacity];
front = 0;
rear = -1;
size = 0;
}
// Method to add an element to the rear of the queue
public void enqueue(int item) {
if (isFull()) {
System.out.println("Queue is full. Cannot enqueue.");
return;
}
rear = (rear + 1) % capacity; // Circular increment
array[rear] = item;
size++;
}
// Method to remove and return the element at the front of the queue
public int dequeue() {
if (isEmpty()) {
System.out.println("Queue is empty. Cannot dequeue.");
return -1;
}
int removedItem = array[front];
front = (front + 1) % capacity; // Circular increment
size--;
return removedItem;
}
// Method to return the element at the front of the queue without removing it
public int peek() {
if (isEmpty()) {
System.out.println("Queue is empty. Cannot peek.");
return -1;
}
return array[front];
}
// Method to check if the queue is empty
public boolean isEmpty() {
return size == 0;
}
// Method to check if the queue is full
public boolean isFull() {
return size == capacity;
}
// Method to return the size of the queue
public int size() {
return size;
}
// Method to display the elements of the queue
public void display() {
if (isEmpty()) {
System.out.println("Queue is empty.");
return;
}
System.out.print("Queue: ");
int index = front;
for (int i = 0; i < size; i++) {
System.out.print(array[index] + " ");
index = (index + 1) % capacity; // Circular increment
}
System.out.println();
}
// Main method for testing
public static void main(String[] args) {
ArrayQueue queue = new ArrayQueue(5);
queue.enqueue(1);
queue.enqueue(2);
queue.enqueue(3);
queue.display(); // Queue: 1 2 3
System.out.println("Dequeued: " + queue.dequeue()); // Dequeued: 1
System.out.println("Peeked: " + queue.peek()); // Peeked: 2
queue.enqueue(4);
queue.enqueue(5);
queue.enqueue(6); // Queue is full. Cannot enqueue.
queue.display(); // Queue: 2 3 4 5
}
}This implementation includes methods for enqueue, dequeue, peek, isEmpty, isFull, size, and display. Circular increment is used for rear and front pointers to make the queue circular and utilize the array efficiently.
B. Linked List-based Implementation
Linked List-based Queue Implementation
Overview:
A linked list-based queue uses a linked list data structure to implement the queue operations. Each node in the linked list represents an element in the queue, and pointers are used to maintain the front and rear of the queue. Elements are added to the rear and removed from the front, adhering to the FIFO principle.
Operations and Their Time Complexities:
- Enqueue (Addition):
- Description: Adds an element to the rear end of the queue.
- Implementation: Create a new node with the given element and append it to the end of the linked list.
- Time Complexity: O(1) – Constant time complexity.
- Dequeue (Removal):
- Description: Removes and returns the element at the front of the queue.
- Implementation: Remove the first node from the linked list and update the front pointer.
- Time Complexity: O(1) – Constant time complexity.
- Peek (Examination):
- Description: Retrieves the element at the front of the queue without removing it.
- Implementation: Access the data of the first node in the linked list.
- Time Complexity: O(1) – Constant time complexity.
- isEmpty (Check if Empty):
- Description: Checks if the queue is empty.
- Implementation: Check if the front pointer is null.
- Time Complexity: O(1) – Constant time complexity.
- Size (Get Size):
- Description: Returns the number of elements in the queue.
- Implementation: Traverse the linked list and count the number of nodes.
- Time Complexity: O(n) – Linear time complexity.
Pros:
- Dynamic Memory Management: Linked list-based queues can grow and shrink dynamically without requiring resizing.
- Efficient Enqueue and Dequeue: Adding and removing elements from the front or rear of the linked list is efficient, with constant time complexity.
- No Wasted Memory: Memory is utilized efficiently as nodes are allocated dynamically as needed.
Cons:
- Memory Overhead: Linked list-based queues have additional memory overhead due to the storage of node pointers.
- No Random Access: Direct access to elements by index is not supported, unlike array-based implementations.
- Slower Size Retrieval: Determining the size of the queue requires traversing the entire linked list, resulting in linear time complexity.
Overall, linked list-based queues offer dynamic memory management and efficient enqueue and dequeue operations, making them suitable for scenarios where the size of the queue may vary dynamically. However, they may incur higher memory overhead and slower size retrieval compared to array-based implementations.
C. Comparison between Array-based and Linked List-based Queue Implementation
| Aspect | Array-based Queue | Linked List-based Queue |
|---|---|---|
| Memory Management | Fixed-size array, requires resizing for dynamic growth | Dynamic memory allocation, no resizing needed |
| Enqueue Operation | Constant time complexity (O(1)), with occasional resizing | Constant time complexity (O(1)) |
| Dequeue Operation | Linear time complexity (O(n)) due to element shifting | Constant time complexity (O(1)) |
| Peek Operation | Constant time complexity (O(1)) | Constant time complexity (O(1)) |
| Size Operation | Constant time complexity (O(1)) | Linear time complexity (O(n)) |
| Random Access | Supported, allows direct access to elements by index | Not supported, traversal required for access by position |
| Memory Overhead | Lower, only stores data elements | Higher, stores additional pointers for each node |
| Dynamic Memory Management | Requires resizing for dynamic growth | Can grow and shrink dynamically without resizing |
| Performance (Enqueue/Dequeue) | Slower dequeue operation due to element shifting | Faster dequeue operation due to direct removal of node |
| Usage | Suitable for scenarios with fixed or known maximum size | Suitable for scenarios with dynamic or unknown size |
This comparison highlights the differences between the two implementations regarding memory management, time complexity of operations, memory overhead, dynamic memory management, and suitability for various usage scenarios. Depending on the specific requirements and constraints of an application, either array-based or linked list-based queue implementation may be preferred.
Application of Queue in Data Structure
Queue in data structure find numerous applications across various domains due to their ability to manage data or tasks in a FIFO (First-In-First-Out) manner. Some common applications of queues include:
- Operating System Scheduling: Queues are used in operating systems for task scheduling, managing process execution, and handling I/O requests. Various scheduling algorithms such as Round Robin and First-Come-First-Served (FCFS) utilize queues to manage the order of process execution and resource allocation.
- Network Packet Routing: Queues are essential in networking devices such as routers and switches for managing data packet transmission and routing. They help regulate the flow of network traffic, prevent congestion, and ensure smooth data delivery by buffering packets in queues before forwarding them.
- Print Spooling: Queues are employed in print spooling systems to manage print job requests from multiple users. Print jobs are added to a queue and processed sequentially, allowing for efficient utilization of printing resources and fair access to the printer.
- Task Management in Multitasking Environments: Queues are used in multitasking environments to manage task queues and prioritize task execution. Tasks or threads are added to queues based on their priority or scheduling criteria, ensuring efficient resource allocation and task execution.
- Job Processing in Batch Systems: Queues are utilized in batch processing systems for managing job queues and scheduling batch jobs for execution. Batch jobs are added to queues and processed sequentially, allowing for efficient utilization of computing resources and automated job scheduling.
- Event Handling in GUI Applications: Queues are used in graphical user interface (GUI) applications for event handling and message passing. Events such as mouse clicks, keyboard input, and window messages are added to event queues and processed sequentially, ensuring responsive and interactive user interfaces.
- Buffer Management in Data Streaming: Queues are employed in data streaming applications for buffer management and flow control. Data streams are buffered in queues to smooth out variations in data arrival rates, ensure continuous data processing, and prevent data loss or overflow.
- Call Center Queuing: Queues are used in call center systems to manage incoming calls and customer service requests. Calls are placed in queues and routed to available agents based on predefined criteria such as caller priority, agent availability, and skill matching.
- Simulation and Modeling: Queues are widely used in simulation and modeling applications to represent waiting lines, service processes, and event sequences. They facilitate the modeling of complex systems with dynamic behavior, enabling analysis, optimization, and prediction of system performance.
- Transaction Processing: Queues are utilized in transaction processing systems to manage transaction queues and ensure orderly processing of transactions. Transactions are added to queues and processed sequentially, ensuring data consistency, integrity, and reliability in banking, finance, and e-commerce systems.
These are just a few examples of the diverse applications of Queue in Data Structure across various domains. Queue in Data Structure play a critical role in managing data, tasks, and resources in a wide range of real-world scenarios, contributing to the efficiency, reliability, and performance of systems and applications.
Advanced Queue in Data Structures
Types of queue in data structure
In data structures, queues can be implemented in various ways to suit different requirements and scenarios. Here are some common types of queues:
- Linear Queue:
- A basic queue where elements are inserted at the rear (end) and removed from the front.
- Follows the First-In-First-Out (FIFO) principle.
- Implemented using arrays or linked lists.
- Circular Queue:
- A variation of the linear queue where the rear pointer wraps around to the front when it reaches the end of the queue, forming a circular structure.
- Optimizes space utilization in array-based implementations by reusing the empty spaces left after dequeuing elements.
- Prevents unnecessary shifting of elements, improving performance.
- Priority Queue:
- A queue where each element has a priority associated with it, and elements are dequeued based on their priority rather than their arrival time.
- Higher-priority elements are dequeued before lower-priority ones.
- Implemented using various data structures such as heaps, balanced binary search trees, or arrays.
- Double-Ended Queue (Deque):
- A queue that supports insertion and deletion of elements from both the front and the rear.
- Can function as both a queue and a stack, providing flexibility in various applications.
- Implemented using doubly linked lists or arrays.
- Blocking Queue:
- A thread-safe queue that supports blocking operations like blocking enqueue and dequeue operations.
- Typically used in concurrent programming to facilitate communication and synchronization between threads.
- Priority Blocking Queue:
- A combination of a priority queue and a blocking queue.
- Allows elements to be inserted and removed based on their priority, with blocking operations for thread safety.
- Bounded Queue:
- A queue with a fixed maximum capacity, where attempting to enqueue an element when the queue is full results in an error or blocking behavior.
- Useful for scenarios where resource management and limiting memory usage are crucial.
- Concurrent Queue:
- A queue designed to support concurrent access by multiple threads without the need for explicit synchronization.
- Ensures thread safety and atomicity of operations through lock-free algorithms or other concurrency control mechanisms.
These are some of the common types of queues used in data structures and software development, each offering unique features and capabilities to address different requirements and use cases.
Conclusion
In conclusion, Queue in Data Structure are fundamental data structures that operate on the First-In-First-Out (FIFO) principle, making them essential tools in computer science and various real-world applications. By maintaining the order of elements based on their arrival sequence, queues facilitate orderly processing, efficient resource management, and task scheduling. Throughout this exploration, we’ve delved into the basic concepts, implementations, operations, and applications of queues, highlighting their significance and versatility in diverse domains.
Summary of Key Points
- Queue in data structure adhere to the FIFO (First-In-First-Out) principle, ensuring that the first element added is the first one to be removed.
- Basic operations of queues include enqueue (addition), dequeue (removal), peek (examination), isEmpty (check if empty), and size (get size).
- Implementations of queue in data structure include array-based and linked list-based approaches, each with its own advantages and disadvantages.
- Array-based queues offer efficient random access and fixed-size memory management but require resizing for dynamic growth and incur memory overhead.
- Linked list-based queues provide dynamic memory management, efficient enqueue and dequeue operations, and no resizing overhead but may have slower size retrieval and higher memory overhead.
- Queues find applications in operating system scheduling, network packet routing, print spooling, multitasking environments, GUI event handling, data streaming, call center queuing, simulation, transaction processing, and more.
Future Developments and Applications of Queue in Data Structure
Looking ahead, the development and applications of queue in data structure continue to evolve to meet the growing demands of modern computing and technology. Some potential future developments and applications include:
- Optimization for High-Performance Computing: Enhancing queue algorithms and implementations for efficient processing of large-scale data and high-throughput applications, such as big data analytics, cloud computing, and distributed systems.
- Real-Time Systems and IoT: Integration of queue data structures into real-time systems and Internet of Things (IoT) devices for managing time-critical tasks, event-driven processing, and sensor data streaming in smart environments and industrial automation.
- Advanced Queue Architectures: Exploration and development of advanced queue architectures, such as priority queues, concurrent queues, and lock-free queues, to address specific performance, concurrency, and synchronization requirements in multi-threaded and parallel computing environments.
- Queue-Based Machine Learning Pipelines: Utilization of queues in machine learning pipelines and data processing workflows for efficient data ingestion, feature extraction, model training, and result dissemination, enabling scalable and distributed machine learning systems.
- Blockchain and Decentralized Systems: Adoption of queues in blockchain networks and decentralized systems for transaction queuing, consensus mechanism, and data propagation, supporting scalable, secure, and decentralized applications.
Overall, as computing technologies continue to advance and evolve, the role of queue in data structure remains crucial in enabling efficient data management, task scheduling, and system optimization across a wide range of applications and industries. Continued research, innovation, and application of queue data structures will contribute to the development of more robust, scalable, and responsive computing systems in the future.
FAQs
What is queue in data structure?
A queue in data structure is a linear data structure that follows the First-In-First-Out (FIFO) principle. It stores elements in a sequence where the first element added is the first one to be removed.
What are the basic operations supported by a queue?
The basic operations supported by a queue include:Enqueue: Adds an element to the rear of the queue.
Dequeue: Removes and returns the element at the front of the queue.
Peek: Retrieves the element at the front of the queue without removing it.
isEmpty: Checks if the queue is empty.
Size: Returns the number of elements in the queue.
What are the main applications of queues?
Queues find applications in various domains, including:Operating system scheduling
Network packet routing
Print spooling
Call center queuing
GUI event handling
Transaction processing
Simulation and modeling
Data streaming and buffer management
How are queues implemented?
Queues can be implemented using different data structures, such as arrays or linked lists. Array-based queues use a fixed-size or dynamically resizing array to store elements, while linked list-based queues utilize a linked list structure with nodes to store elements.
What is the difference between stack and queue data structures?
While both stacks and queues are linear data structures, they differ in their access and removal order. Stacks follow the Last-In-First-Out (LIFO) principle, where the last element added is the first one to be removed, while queues follow the FIFO principle.
Can queues be implemented using other data structures?
Yes, queues can also be implemented using other data structures such as doubly linked lists, circular buffers, or priority queues depending on the specific requirements and constraints of the application.
Are queues thread-safe?
It depends on the implementation. In multi-threaded environments, concurrent access to queues can lead to race conditions and data corruption. To ensure thread safety, synchronization mechanisms such as locks or concurrent data structures should be used.
What is a circular queue?
A circular queue is a variation of a queue data structure where the rear pointer wraps around to the beginning of the array when it reaches the end, forming a circular buffer. This allows for efficient use of space and avoids the need for shifting elements during enqueue and dequeue operations.
Read other awesome articles in Medium.com or in akcoding’s posts.
OR
Join us on YouTube Channel
OR Scan the QR Code to Directly open the Channel 👉

